FUNCION CUADRATICA
Una función cuadrática es aquella que puede escribirse de la forma:
f(x) = ax2 + bx + c
donde a, b y c son números reales cualesquiera y a distinto de cero.
Si representamos "todos" los puntos (x,f(x)) de una función cuadrática, obtenemos siempre una curva llamada parábola.
Por ejemplo: f(x) = x2
CORTE CON EL EJE Y
La función corta el eje y en el punto y = f(0), es decir, la parábola corta el eje y cuando x vale cero (0):
- y = f (0) = a. 02 + b.0 + c
lo que resulta:
- y = f (0) = c
la función corta el eje y en el punto (0, c), siendo c el termino independiente de la función.
A este punto de la función también se lo conoce con Ordenada al Origen
Corte con el eje x
La función corta al eje x cuando y vale 0, dada la función:
- y = ax2 + bx + c
tendremos que:
- y = 0 ----- ax2 + bx + c = 0
las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el eje x, que se obtienen como es sabido por la expresión:
donde:
se le llama discriminante, Δ:
según el signo del discriminante podemos distinguir:
DISCRIMINANTE POSITIVO
Δ > 0, la ecuación tiene dos soluciones, y por tanto la parábola cortara al eje x en dos puntos: x1 y x2.Veamos por ejemplo la función:
que cortara el eje x cuando:
que tendrá por solución general:
en este caso:
que resulta:
Para esta ecuación el discriminante tiene valor positivo:
y por tanto tiene dos soluciones:
operando:
Los puntos: (-1,0), (5,0) son los de corte con el eje x, como se puede ver en la figura.
DISCRIMINANTE NULO
Δ = 0, la ecuación tiene una única solución en x1, la parábola solo tiene un punto en común con el eje x, el cual es el vértice de la función donde las dos ramas de la parábola confluyen.
si la función cuadrática:
que cortara al eje de las x si:
su solución sera:
Operando los valores, tendremos:
la raíz de cero es cero, luego el discriminante en este caso vale cero, y habrá una única solución:
El punto de corte de la función con el eje de las x es (2,0), que en este caso es tangencial de la función con el eje, ver figura.
DISCRIMINANTE NEGATIVO
Δ < 0, la ecuación no tiene solución real, y la parábola no corta al eje x.
Si tenemos la función siguiente:
que corta el eje x cuando:
para encontrar su solución haremos:

Haciendo las operaciones, tendremos:
Al no existir ningún número real que sea la raíz de –8, no se puede continuar haciendo las operaciones, por lo que podemos decir que esta función no tiene corte con el eje x, como se ve en la figura.
Si tenemos en cuenta la existencia de los números imaginarios, podemos realizar las siguientes operaciones:
Continuando con las operaciones:
dando como solución:
Dado el plano cartesiano xy, real, la parábola vista no corta el eje real x en ningún punto, esa misma ecuación estudiada dentro de los números complejos presenta dos soluciones, cumpliéndose de este modo el Teorema fundamental del álgebra.
A la/s intersección/es de la gráfica de la función con el eje x se las llama Ceros o Raíces de la función
EXTREMOS RELATIVOS
Para localizar los extremos relativos, se calcula la derivada de la función, y se iguala a cero, la solución a esta ecuación son los posibles máximos y mínimos de la función, en este caso, partiendo de la función cuadrática:
calculamos su derivada respecto a x:
que si la igualamos a cero, tenemos:
donde x valdrá:
En la vertical que pasa por este valor de x se encontrar el valor máximo o mínimo relativo de la función.
Para saber si es un máximo o un mínimo es necesario ver la derivada segunda de la función, veamos:
esto es: 2a sera positivo cuando a sea positivo y negativo si a es negativo, por tanto, si la derivada segunda 2a es positiva la parábola es cóncava y el punto será un mínimo de la función, si a es negativa la parábola será convexa y sea un máximo.
FORMA FACTORIZADA
Toda función cuadrática se puede factorizar en función de sus raíces. Dada:
se puede factorizar como:
- F(x) = a(x-x1)(x-x2)
siendo a el coeficiente principal de la función, por ello se extrae siempre como factor común, de no escribirse, el coeficiente de x2 sería siempre 1. x1 y x2 representan las raíces de f(x). En el caso de que el Discriminante Δ sea igual a 0 entonces x1 = x2 por lo que podríamos escribir:
En este caso a x1 se la denomina raíz doble, ya que su orden de multiplicidad es 2.
FORMA CANONICA
Toda función cuadrática puede ser expresada mediante el cuadrado de un binomio de la siguiente manera:
A esta forma de expresión se la llama forma canónica. Siendo a el coeficiente principal y el par ordenado (h;k) las coordenadas del vértice de la parábola. Para llegar a esta expresión se parte de la forma polinómica y se realiza el siguiente procedimiento:
- Dado: F(x) = ax2 + bx + c
- Se extrae a como factor común en el término cuadrático y en el lineal.
- Se completa el trinomio cuadrado perfecto, sumando y restando para no alterar la igualdad.
- Se factoriza formando el cuadrado de un binomio.
- sustituyendo:
- la expresión queda:
FUNCION EXPONENCIAL
La función exponencial, es conocida formalmente como la función real ex, donde e es el número de Euler, aproximadamente 2.71828.... Esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma
siendo  números reales,
números reales,  . Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.
. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.
 números reales,
números reales,  . Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.
. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.DEFINICION FORMAL
La función exponencial ex puede ser definida de diversas maneras equivalentes entre sí, como una serie infinita. En particular puede ser definida como una serie de potencias:
o como el límite de la sucesión:
PROPIEDADES
La función exponencial (y exponenciales en base distinta a e) satisfacen las siguientes propiedades generales.
- Son las únicas funciones que son igual a su derivada (multiplicada por una constante, en el caso de que tengan una base distinta a e)
- su límite en - ∞ es 0, y en + ∞ es + ∞
DERIVADA
La importancia de las funciones exponenciales en matemática y ciencias radica principalmente de las propiedades de su derivada. En particular,
Es decir, ex es su propia derivada. Es la única función con esa propiedad (sin tomar en cuenta la multiplicación de la función exponencial por una constante). Otras formas de expresar lo anterior:
- La pendiente del gráfico en cualquier punto es la altura de la función en ese punto.
- La razón de aumento de la función en x es igual al valor de la función en x.
- La función es solución de la ecuación diferencial y' = y.
Si la base de la exponencial no es el número e, sino otro número real arbitrario a mayor que 0, entonces la derivada de ésta es:
donde la función ln denota el logaritmo natural.
DEFINICION PARA NUMEROS COMPLEJOS
Como en el caso real, la función exponencial puede ser definida como una función holomorfa en el plano complejo de diferentes maneras. Algunas de ellas son simples extensiones de las fórmulas que se utilizan para definirla en el dominio de los números reales. Específicamente, la forma más usual de definirla para el dominio de los números complejos es mediante la serie de potencias, donde el valor real x se sustituye por la variable compleja z:
para valores imaginarios puros se cumple la identidad
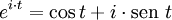 ,
,
en el que un caso particular es la identidad de Euler, conocida también como la fórmula más importante del mundo.
Usando la identidad anterior, donde ahora z=x+yi, con x e y números reales, se obtiene una definición equivalente a la primera,
relación que demuestra que esta función, además de ser holomorfa, es periódica, con un periodo para la parte imaginaria de 2πi.
ECUACIONES
Una ecuación es una igualdad matemática entre dos expresiones algebraicas, denominadas miembros, en las que aparecen valores conocidos o datos, y desconocidos o incógnitas, relacionados mediante operaciones matemáticas. Los valores conocidos pueden ser números, coeficientes o constantes; y también variables cuya magnitud se haya establecido como resultado de otras operaciones. Las incógnitas, representadas generalmente por letras, constituyen los valores que se pretende hallar. Por ejemplo, en la ecuación:
La letra x representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. Resolver una ecuación es encontrar su dominio solución, que es el conjunto de todos los valores de las incógnitas para los cuales la igualdad se cumple; y se llama solución de una ecuación a cualquier valor individual de dichas variables que la satisfaga. Para el caso dado, la solución es:
Todo problema matemático puede expresarse en forma de una o más ecuaciones. Sin embargo no todas las ecuaciones tienen solución, ya que es posible que no exista ningún valor de la incógnita que haga cierta una igualdad dada. También puede ocurrir que haya varios o incluso infinitos conjuntos de valores que la satisfagan.
En el caso de que todo valor posible de la incógnita haga cumplir la igualdad, la expresión se llama identidad. Si en lugar de una igualdad se trata de una desigualdad entre dos expresiones matemáticas, se denominará inecuación. Una ecuación funcional es aquella en la que algunas de las constantes y variables que intervienen no son realmente números sino funciones; y si en la ecuación aparece algún operador diferencial se llama ecuación diferencial.
ECUACION POLINOMIAL
Una ecuación polinomial o polinómica es una igualdad entre dos polinomios. Por ejemplo:
FORMA CANONICA
Realizando una misma serie de transformaciones en ambos miembros de una ecuación, puede conseguirse que uno de ellos se reduzca a cero. Si además se ordenan los términos según los exponentes a los que se encuentran elevadas las incógnitas, de mayor a menor, se obtiene una expresión denominada forma canónica de la ecuación. Frecuentemente suele estudiarse a las ecuaciones polinómicas a partir de su forma canónica, es decir aquella cuyo primer miembro es un polinomio y cuyo segundo miembro es cero.
En el ejemplo dado, sumando 2xy y restando 5 en ambos miembros, y luego ordenando, obtenemos:
GRADO
Se denomina grado de una ecuación polinomial al mayor exponente al que se encuentran elevadas las incógnitas. Por ejemplo
Es una ecuación de tercer grado porque la variable x se encuentra elevada al cubo en el mayor de los casos.
Las ecuaciones polinómicas de grado n de una sola variable sobre los números reales o complejos, pueden resolverse por el método de los radicales cuando n < 5 (ya que en esos casos el grupo de Galois asociado a las raíces de la ecuación es soluble). La solución de la ecuación de segundo grado es conocida desde la antigüedad; las ecuaciones de tercer y cuarto grado se conocen desde los siglos XV y XVI, y usan el método de radicales. La solución de la ecuación de quinto grado no puede hacerse mediante el método de radicales, aunque puede escribirse en términos de la función theta de Jacobi.
ECUACION DE PRIMER GRADO
Se dice que una ecuación polinomial es de primer grado cuando la variable (aquí representada por la letra x) no está elevada a ninguna potencia, es decir que su exponente es 1.
Las ecuaciones de primer grado tienen la forma canónica:
con a diferente de cero.
Su solución es sencilla: 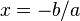
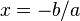
RESOLUCION DE ECUACIONES DE PRIMER GRADO
Las ecuaciones polinómicas de primer grado se resuelven en tres pasos: transposición, simplificación y despeje, desarrollados a continuación mediante un ejemplo.
Dada la ecuación:
TRANSPOSICION
Primero se agrupan todos los monomios que incluyen la incógnita x en uno de los miembros de la ecuación, normalmente en el izquierdo; y todos los términos independientes (los que no tienen x) en el otro miembro. Podemos hacerlo teniendo en cuenta que:
Si sumamos o restamos un mismo monomio en los dos miembros, la igualdad no varía. |
En términos coloquiales, decimos: si un término está sumando (como 16x en el miembro de la derecha) pasa al otro lado restando (−16x a la izquierda); y si está restando (como el −9 de la izquierda), pasa al otro lado sumando (+9 a la derecha)
La ecuación quedará entonces así:
Como puede verse, todos los términos que poseen la variable x han quedado en el primer miembro (a la izquierda del signo igual), y los que no la poseen, por ser sólo constantes numéricas, han quedado a la derecha.
SIMPLIFICACION
El siguiente paso es convertir la ecuación en otra equivalente más simple y corta.
Realizamos la simplificación del primer miembro: 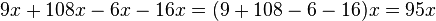
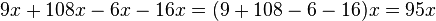
Y simplificamos el segundo miembro: 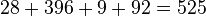
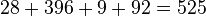
La ecuación simplificada será:
DESPEJE
Ahora es cuando llegamos al objetivo final: que la incógnita quede aislada en un miembro de la igualdad. Para lo cual recordamos que:
Si multiplicamos o dividimos ambos miembros por un mismo número, la igualdad no varía. |
En términos coloquiales: Para despejar la x, si un número la está multiplicando (Ej: 5x) se lo pasa al otro lado dividiendo (n/5) sin cambiar su signo. Y si un número la está dividiendo (Ej: x/2), entonces se lo pasa al otro lado multiplicando (n×2) sin cambiar su signo.
En la ecuación debemos entonces pasar el número 95 al otro miembro y, como estaba multiplicando, lo hará dividiendo, sin cambiar de signo:
El ejercicio está teóricamente resuelto, ya que tenemos una igualdad en la que x equivale al número 525/95. Sin embargo, debemos simplificar.
Resolvemos la fracción (numerador dividido entre denominador) en caso de que el resultado diera exacto; si diera decimal, simplificamos la fracción y ése es el resultado.
En la ecuación, vemos que el resultado de la fracción es decimal (525:95 = 5,5263157894737)
Por tanto, simplificando, la solución es:
ECUACIONES DE SEGUNDO GRADO
Las ecuaciones polinómicas de segundo grado tienen la forma canónica
Donde a es el coeficiente del término cuadrático (aquel en que la incógnita está elevada a la potencia 2), b es el coeficiente del término lineal (el que tiene la incógnita sin exponentes, o sea que está elevada a la potencia 1), y c es el término independiente (el que no depende de la variable, o sea que está compuesto sólo por constantes o números) Todas las ecuaciones de segundo grado tienen dos soluciones, aunque a veces ambas pueden coincidir entre sí. Para su resolución tenemos que distinguir entre tres situaciones distintas:
ECUACIONES DE LA FORMA x² + c = 0
Son un caso particular de ecuaciones de segundo grado en las que no existe el término lineal o término en x, lo que les confiere su principal característica algebraica: el coeficiente b es nulo (b = 0). Esto hace que sea un tipo de ecuaciones muy sencillas de resolver mediante un método similar a las de primer grado. Tengamos por ejemplo:
Donde a = 1 y c = −16. Pasamos entonces −16 al segundo miembro:
Ahora pasamos el exponente 2, o cuadrado, al segundo miembro, convirtiéndolo en la operación opuesta, raíz cuadrada:
La ecuación ya está resuelta.
- Nota: si −c/a fuera un número real negativo (cosa que no ocurre en este caso, donde es −c/a = 4) las raíces de la ecuación serían imaginarias y pertenecerían al campo de los números complejos.
ECUACIONES DE LA FORMA ax² + bx = 0
Son otro caso particular de ecuaciones de segundo grado, en las que no existe el término independiente. En ellas todos los términos dependen de la variable incógnita o, coloquialmente, tienen x, lo que les confiere también una característica algebraica: el coeficiente c es nulo (c = 0). Tengamos:
Donde a = 3 y b = 9. En este tipo de ecuaciones, lo primero que hacemos es declarar x como factor común de ambos términos:
Esta expresión es una multiplicación cuyo resultado es 0; por lo tanto, uno de los dos factores tiene que ser igual a 0. Así es que, o el primer factor (x) es igual a cero (lo que constituye una de las soluciones), o lo es el segundo:
Por lo tanto, las dos soluciones válidas para esta ecuación son 0 y −3.
ECUACIONES DE LA FORMA ax² + bx + c = 0
Son el caso más general de ecuaciones de segundo grado, en el que existen los tres términos: cuadrático, lineal e independiente. Los tres coeficientes a, b y c serán entonces no nulos o distintos de cero.
Si tenemos la ecuación cuadrática: 

Para resolver ecuaciones cuadráticas utilizamos la fórmula general:
Si sustituimos las letras por los números, siendo:
- a = coeficiente de la incógnita elevada al cuadrado con su signo.
- b = coeficiente de la incógnita elevada a uno.
- c = coeficiente de la incógnita elevada a cero (el número libre).
A partir de esta fórmula obtenemos las soluciones de esta ecuación, que son: -2 y -3
Si el resultado obtenido dentro de la raíz es un número negativo, las soluciones son números complejos.
OTRO METODO
También podemos resolver ecuaciones cuadráticas del siguiente modo:
Si hallamos dos números m y n tales que al sumarlos y multiplicarlos entre sí resulten coincidir respectivamente con −b y c, entonces la expresión:
será equivalente a:
siendo m y n los dos valores (o raíces) de la expresión.
En el ejemplo anterior, m = -2 y n = -3, puesto que: 2 + 3 = 5 y 2 × 3 = 6.
luego, la igualdad:
es equivalente a:
DEMOSTRACION
Partiendo de la igualdad: 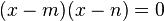
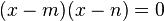
operando, obtenemos: 

Luego, para a = 1, resulta:
m y n son por lo tanto dos números cuya suma resulta igual a −b, y cuyo producto coincide con c.
TIPOS DE ECUACION ALGEBRAICA
Una ecuación algebraica en x contiene solo expresiones algebraicas, como polinomios, expresiones racionales, radicales y otras. Una ecuación de este tipo se llama ecuación condicional si hay números en los dominios de las expresiones que no sean soluciones; por ejemplo, x^2= 9 es condicional porque el número x=4 (y otros) no es una solución. Si todo número de los dominios de las expresiones de una ecuación algebraica es una solución, la ecuación se llama identidad.
FUNCIONES LOGARITMICAS
Las inversas de las funciones exponenciales se llaman funciones logarítmicas. Como la notación f-1 se utiliza para denotar una función inversa, entonces se utiliza otra notación para este tipo de inversas. Si f(x) = bx, en lugar de usar la notación f-1(x), se escribe logb (x) para la inversa de la función con base b. Leemos la notación logb(x) como el “logaritmo de x con base b”, y llamamos a la expresión logb(x) un logaritmo.
Definición: El logaritmo de un número y es el exponente al cual hay que elevar la base b para obtener a y. Esto es, si b > 0 y b es diferente de cero, entonces
logb y = x si y sólo si y = bx.GRAFICAS DE FUNCIONES LOGARITMICAS
Las funciones y = bx y y = logb x para b>0 y b diferente de uno son funciones inversas. Así que la gráfica de y = logb x es una reflexión sobre la recta y = x de la gráfica de y = bx. La gráfica de y = bx tiene como asíntota horizontal al eje de x mientras que la gráfica de y = logb x tiene al eje de y como asíntota vertical.
Ejemplo:


y = 2x y = log2 x
Las funciones y = 2x y y = log2 x son funciones inversas una de la otra, por tanto, la gráfica de y = log2 x es una reflexión de la gráfica de y = 2x sobre la recta y = x. El dominio de y = 2x es el conjunto de los números reales y el recorrido es todos los números reales mayores que cero. El dominio de y = log2 x es el conjunto de los números reales mayores que cero y el recorrido el conjunto de los números reales.





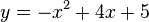
















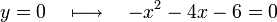
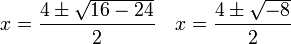








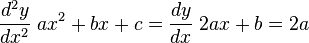







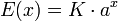
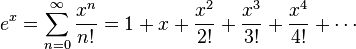





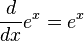



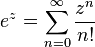


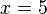



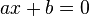
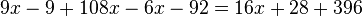
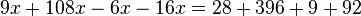

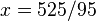



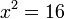
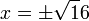

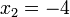
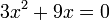



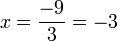
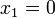

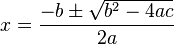


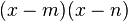

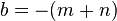
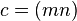
Impecable!
ResponderEliminar